HTML 5 Canvas: кривая дракона

1 комментарий
Кривая дракона

Кривая дракона

Кривая дракона — общее название для некоторых кривых фрактальных , которые могут быть аппроксимированы рекурсивными методами, такими как L-системы. Дракон Хартера, также известный как дракон Хартера — Хейтуэя, был впервые исследован физиками NASA — John Heighway, Bruce Banks, и William Harter. Он был описан в 1967 году Мартином Гарднером (Martin Gardner).

Естественно, рисовать буду на Canvas :3

L-системы, к слову, иначе называются переписываемыми алгоритмами генерации математических структур. Данный тип алгоритмов был предложен в 1904 году математиком Хельгой фон Кох (H. von Kokh) (снежинка Коха). В конце пятидесятых годов Хомский использовал эти алгоритмы для описания формальных грамматик. Кто изучал трансляторы, тот понимает о чём речь.

Кривая дракона

Кривая дракона — это кривая без самопересечений, которая определяется рекурсивно. Интересовал больше математический аспект. Ну, как обычно, используется формула для поворота точки относительно другой точки: Поворот точки относительно другой точки

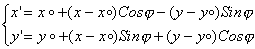
Когда начал реализовывать фрактал, то сначала хотел запоминать точки на каждой итерации. Затем хотел сделать рекурсию, для нахождения точки (то есть смотреть предыдущие итерации сначала). В итоге, реализовал так же как снежинку Коха.

Решил закономерность выявить, как же изгибается линия. Когда влево, а когда вправо. В итоге, закономерность была найдена. В зависимости от номера линии, определяем знак. Это потом необходимо для вычисления угла поворота следующей точки. 

this.sign= function(i)
{
  var j = i;
  while(true)
  {
    if ((j-1) % 4 == 0) return -1;
    else 
      if ((j-3) % 4 == 0) return 1;
      else j=j/2;
					

  }
}

Собственно, вот. 

a =((a - 90*this.sign(i))+a)%360;

Уже после того, как допёр сам, нашёл в инете логику эту =_= Описать эту кривую можно, задавая поворот налево цифрой 1, а поворот направо — цифрой 0. Важно, что все повороты совершаются на один и тот же угол.

Порядком кривой дракона называется количество звеньев получающейся ломаной. Кривая первого порядка определяется просто как 1. Для кривых более высоких порядков справа приписываем 1, а затем дополняеся цифрами, которые стоят левее этой единицы справа налево, записывая их слева направо, но только заменяем нули на единицы, а единицы на нули.

Как пример, кривая второго порядка: сначала 1, приписываем справа 1: 11, а теперь справа добавляем единицу, замененную на нуль, получаем 110. Кривая третьего порядка: берем 110, приписываем справа единицу: 1101, а теперь добавляем число, которое стоит слева от последней единицы (это 110), записанное в обратном порядке (011), заменяя нули на единицы и обратно, т.е. число 100, получаем 1101100. Для четвёртого: 110110011100100.

Сам поворот: 

 this.pointRotation= function(x1,y1,x2,y2,a)
{
  var resx = x1+(x2-x1)*Math.cos(a*Math.PI/180)-(y2-y1)*Math.sin(a*Math.PI/180);	
  var resy = y1+ (x2 - x1)*Math.sin(a*Math.PI/180)+(y2-y1)*Math.cos(a*Math.PI/180);
  return {x:resx, y:resy};
}

В первом случае рисуются все итерации, и показано как изгибаются линии на следующей итерации.

HTML5 нид, мэн

Во втором случае рисуется только конечная итерация.

HTML5 нид, мэн

Если интересно, можете покопаться в исходнике.