Кривая Коха — фрактальная кривая, описанная в 1904 году шведским математиком Хельге фон Кохом. Три копии кривой Коха, построенные (остриями наружу) на сторонах правильного треугольника, образуют замкнутую кривую, называемую снежинкой Коха.

У меня порой бывают заскоки, когда хочется какую-то мат. задачку запрограммировать. На этот раз решил с фракталами повозиться. А именно со снежинкой Коха.

Снежинка Коха

Этот фрактал — один из первых исследованных учёными. Он получается из трёх копий кривой Коха, которая впервые появилась в статье шведского математика Хельге фон Коха в 1904 году. Эта кривая была придумана как пример непрерывной линии, к которой нельзя провести касательную ни в одной точке.

Основные свойства кривой Коха:

1. Она непрерывна, но нигде не дифференцируема.
2. Имеет бесконечную длину. Пусть длина исходного отрезка равна 1. На каждом шаге построения мы заменяем каждый из составляющих линию отрезков на ломаную, которая в 4/3 раза длиннее. Значит, и длина всей ломаной на каждом шаге умножается на 4/3: длина линии с номером n равна (4/3)n–1. Поэтому предельной линии ничего не остается, кроме как быть бесконечно длинной.
3. Снежинка Коха ограничивает конечную площадь. И это при том, что ее периметр бесконечен. Это свойство может показаться парадоксальным, но оно очевидно — снежинка полностью помещается в круг, поэтому ее площадь заведомо ограничена.

Немного математики

Довольно интересно иногда вспомнить простейшие мат. преобразования (: В данном случае необходимо было освежить знания о векторах и трансформации точек в плоскости.

В частности, как повернуть точку относительно другой точки:

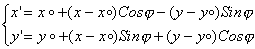
Ну и необходимо знать, как найти точку на отрезке, отдалённую на какое-то расстояние от точки, зная это расстояние и координаты точек. Методов так-то много. Можно найти координаты прямой, содержащую точки эти, а потом подставлять в уравнение. Можно вычислить координаты, используя вектора.

Выглядит как-то так: